The Center on Education Policy released a disturbing new study this week, measuring the effects of No Child Left Behind:

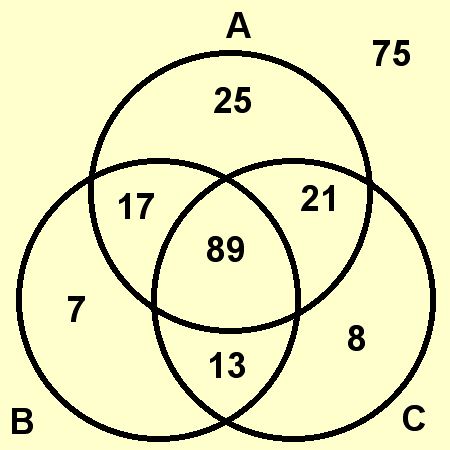
The report finds that approximately 62% of school districts increased the amount of time spent in elementary schools on English language arts and or math, while 44% of districts cut time on science, social studies, art and music, physical education, lunch or recess.

Now, I’m pretty much appalled by all of the cutbacks, but I’ll leave the bulk of it to ScienceTeacher.com, SocialStudiesTeacher.com, and LunchTeacher.com. I’m ShakespeareTeacher.com, so I want to talk about arts education.

(And let’s make no mistake – the extra time being spent on ELA isn’t being spent on literature. It’s being spent on test prep, and more test prep.)

Arts education is absolutely essential for students preparing for the world that we’re currently living in. With the image continuing to gain dominance over the written word, people who can demonstrate artistic ability are highly marketable in today’s economy. From graphic designers to documentary filmmakers, those who can master today’s tools of communication are able to command a wider audience and expand their range of communication. In the connected world, this is real currency.

And even if all of that weren’t true, the arts teach us how to identify problems and solve them with creativity and discipline. Those skills help us in any endeavor.

I came across a website for an artist named Jen Stark, who creates sculptures from construction paper that won’t help anyone pass a reading test any time soon. But they bring beauty into the world, which is worth at least a link from my blog. Take a look at her work, and tell me she didn’t have to develop some pretty sophisticated math skills along the way.

Or take French artist Huber Duprat, who recruited caddis fly larvae, who typically create protective shells out of silk and their surrounding materials, and placed them in an environment of gold flakes and precious gems. The result is a combination of art and science that boggles the mind. Click the picture below to see the video.

Or take a look at the Universcale by Nikon, an application of the mathematics of scale to allow human comprehension of the natural universe, and tell me your appreciation of it isn’t primarily aesthetic.

I wonder what Leonardo DaVinci would have thought about eliminating arts education to teach math. What would Shakespeare have thought about eliminating arts education to teach literacy? What would Descartes say about eliminating science to teach math? What would Hemmingway think of eliminating social studies to teach literacy?

Reading and math are important skills. But even if an educational system were somehow able to acheive 100 percent literacy and numeracy, and nothing else, it would still be a failure.

I often like to come up with games of chance. There have been times in my life when this has been profitable, but mostly I’m just interested in questions of statistics and probability.

I had considered the math behind putting together my own Deal or No Deal style game, but with greatly reduced suitcase amounts and with a cost to play. Determining a fair cost (one which I would agree to if I were the player or the banker) at first seems like a hopelessly difficult problem, but the math is actually quite simple. The player has the option of keeping the initial suitcase until the end, and the banker has the option of offering whatever small amount he wants. At any given time the chosen suitcase is worth the average of all unopened cases. The banker certainly isn’t going to offer more, and if the player accepts less it’s just because he’s hedging his bets. The cost to play should be the average of all of the cases, whatever they may be.

A couple of months ago, while discussing the Two Envelopes problem, we briefly discussed what’s known as the Monty Hall problem, after the host of Let’s Make A Deal. Thinking of that problem has inspired another gambling proposition which is this week’s Conundrum.

Let’s continue to call our two gamblers the banker and the player. The banker has three boxes and hides a $10 bill in one of the boxes and a $1 bill in each of the other two. The player pays a set amount to the banker and chooses one of the three boxes. The banker must then open one of the other two boxes and show the player a $1 bill. Then the player can decide whether to keep the contents of the box he chose or switch to the other unopened box.

What would be the fair amount for the player to pay the banker to play this game?

UPDATE: Question solved by David. See comments for the answer.

How do they calculate the digits of pi?

I mean, they’ve calculated the number out to billions of places. When they get a billion digits out, how do they know they’re right? Just think about how incredibly precise that is. A quark’s diameter can be described in 18 decimal places, so surely a billion places is far beyond the realm of any practical scientific purpose or authentic human experience.

From a purely mathematical standpoint, pi is defined as the ratio between a circle’s circumference and its diameter. But the only way we have of measuring such things mathematically is by using pi.

Wikipedia has this article on the subject, but I doubt you’ll be surprised when I tell you it is not helpful to me. We could ask Daniel Tammet but he’d probably just tell us what the algorithm tastes like.

Anyway, if all this math stuff is boring to you, check out this discussion thread putting a more philosophical spin on the digits of pi:

“Somewhere inside the digits of pi is a representation for all of us — the atomic coordinates of all our atoms, our genetic code, all our thoughts, all our memories. Given this fact, all of us are alive, and hopefully happy, in pi. Pi makes us live forever. We all lead virtual lives in pi. We are immortal.” – Cliff Pickover

This means that we exist in pi, as if in a Matrix. This means that romance is never dead. Somewhere you are running through fields of wheat, holding hands with someone you love, as the sun sets — all in the digits of pi. You are happy. You will live forever.

Silly, perhaps, but technically true. And somewhere in the digits of pi, there’s a version of the Shakespeare Teacher who understands how they calculate the digits of pi.

When I first started this blog, one of my very first posts suggested that almost all of the current natives of Mongolia and China were probably descendants of Genghis Khan. I literally had no readers at the time – I hadn’t yet told anyone about the blog – and so there was nobody to challenge my sweeping statement. I didn’t even make an argument. I’d like to give my argument now, and reopen the question as a Conundrum.

The idea was based on a National Geographic article about the biological legacy of Genghis Khan:

An international group of geneticists studying Y-chromosome data have found that nearly 8 percent of the men living in the region of the former Mongol empire carry y-chromosomes that are nearly identical. That translates to 0.5 percent of the male population in the world, or roughly 16 million descendants living today.

I went on to note:

16 million descendants. And that’s only men descended from Khan directly through the male line, father to son, for the past 800 years. The total number of Khan’s descendants living today is truly incalculable.

If you figure an average of four generations per century, that’s 32 generations between Genghis and his living descendants. Each person living today should have around 2 to the power of 32, or roughly 4.3 billion, living ancestors that are contemporary with Khan. Obviously, many individuals will have to be counted more than once, so let’s take a different tack.

Let’s pick a year somewhere between 1200 and 2000, say 1500. The total population of mainland Asia in 1500 was 268,400,000. Each living person today would have approximately 2 to the power of 20, or about a million, ancestors who were around in 1500 (and that’s if we don’t count anyone with a living parent).

So how many of the 268,400,000 around in 1500 were Khan’s descendants? Well, there are 16 million men living today that share the Y chomosome. If Khan and his direct male heirs had an average of 1.68 sons over 32 generations, that would give us our 16 million. That would only account for 505 men carrying that Y chromosome in 1500. But that calcuation leaves out two factors.

First, by 1500, Khan’s seed had been pretty well spread. The factors that account for his prevalence today came mostly into play during Khan’s life and the few generations following (see the article for details). So the distribution was a lot more top-heavy than the calculation above would suggest.

Second, we’re only counting direct male-line heirs. Passing a Y chromosome down from father to son over 32 generations is only one of 4.3 billion different permutations of inheritance. Each of those 16 million Y chromosome carriers alive today probably has an average of at least one sister or daughter. That doubles the known descendants right there. Extend that back over 32 generations, then consider all of their descendants, and you get the idea. If we change “average of 1.68 sons over 32 generations” (which we know is true) to “average of 2 children of either sex over 32 generations” (which doesn’t seem like too great of a leap from there), then 16 million becomes 4.3 billion, greater than the population of mainland Asia today.

It seems to me that today’s ethnic Mongolians and Chinese would almost all have to be descended from Khan, some many times over.

Now I am no math expert. I’m a Shakespeare Teacher. It’s very possible I could be wrong about this. I’d be interested to hear what other people think, particularly people with more professional experience with statistical analysis.

And I should also point out that I pin no political, moral, or judgmental significance to being a descendant of Genghis Khan. This is simply a math, history, and logistical Conundrum. I truly hope no offense is taken (though if you read my original post and the Economist article it is based on, it actually seems to be a point of pride for both Mongolia and China to be the descendants of Khan). And my family comes from Belarus, so this would mean I’m probably a descendant of Khan as well. So don’t screw with me.

Now, with all that in mind, for this week’s Conundrum, I hereby submit my original conclusion up for public scrutiny:

So, China and Mongolia should probably stop arguing over which of their people are the true heirs of Genghis Khan. My guess is, almost all of them are.

In a Venn Diagram puzzle, there are three overlapping circles, marked A, B, and C. Each circle has a different rule about who or what can go inside. The challenge is to guess the rule for each circle. You can find a more detailed explanation of Venn Diagram puzzles, along with an example, here.

You’ve told me that there’s not enough math on this site, and I have listened. Each of the eight items below is a number.

Have you figured out one of the rules? Two? All three? Feel free to post whatever you’ve got in the comments below. Just tell us which circle you’re solving, and what the rule is.

Enjoy!

UPDATE: Circles B and C solved by Kenneth W. Davis. See comments for all answers.

Below is a graph of the hits to Shakespeare Teacher for each day of the past month. This reflects the number of unique visitors, not how many pages they viewed.

Visually savvy readers may notice a bit of a spike in yesterday’s readership. Was it the new design? Was it the Conundrum, asking for words that end in -ly? Is the world finally starting to take an interest in Shakespeare lists, Venn Diagram puzzles, and Animaniacs cartoons? Or was it the link from Showtime?

We could sit around all day debating the different theories. The point is that I just got my 2,000th hit while writing this, and over six percent of those hits came in yesterday. Now I think I’ll post a video clip from Sesame Street.

I overheard this once on a train and was never able to figure it out. Maybe someone here can help me.

Imagine I have two envelopes and I tell you truthfully that both contain money and that one envelope contains twice as much money as the other. I offer you your choice of envelope and you choose one of them without opening it.

Now I ask you if you would like to switch envelopes. You chose yours randomly, so it’s a 50/50 chance whether the other envelope contains half as much or twice as much. So, if the amount you now have is x, there’s a 50 percent chance that switching would get you 2x and a 50 percent chance it will get you x/2. You have twice as much to gain as you have to lose, regardless of how much is in your envelope, so it makes sense mathematically to switch envelopes.

But of course, this is ridiculous, since you have no new information about the two envelopes than you had before. Once you’ve made that switch, by the same logic, you should want to switch again. This much seems obvious. So where’s the flaw in the math above?

By the way, I consulted our good friend Wikipedia before posting this, and it was little help. It just mumbled something about Bayesian Decision Theory and said the problem would be easy if I were a mathematician. It then went on to pose a harder problem in which you can look inside one of the envelopes, and an even harder problem that was way over my head at 5:30 am. Thanks, Wikipedia.

Here’s a good example of a high school English teacher using a blog to post and collect student assignments. This is one sample assignment for students in the middle of reading A Midsummer Night’s Dream:

Your assignment now is to take this mixed-up love mess and bring it to a conclusion with a happy ending. As it stands right now, everything is messed up and needs resolution. Assume the role of a narrator and finish the story. This is your chance to predict how this all turns out in the real play.

The students can now write a response to this and read what others have written as well. It seems like a lot of this is going on at home, but as more and more schools adopt one-to-one computing environments (something I’ve personally been very active in for the past year and a half), the more this sort of thing will become commonplace classroom practice.

This presentation from Karl Fisch has been making the rounds.

Students entering kindergarten this September will graduate from high school in 2020. How will the world be run then? How old will you be in that year? It’s not really that far off, is it?

Discuss.

Via Prospero’s Books, I found this article about robots being used to simulate evolution. I’ve read about similar projects simulating evolution through competing artificial intelligence programs, using the “Prisoner’s Dilemma” scenario as the competitive task. The Prisoner’s Dilemma, for those who are unfamiliar, breaks down as some variation of this:

You and a partner are both correctly arrested for two crimes, one major and one minor, and are put in separate rooms. Executive Assistant District Attorney Jack McCoy comes to visit you and offers you a deal: testify against your partner for the major crime, your partner will get twenty years, and you’ll walk for both crimes. However, his lovely assistant is right now offering the same deal to your partner. If you both confess, you’ll both get five years. If your partner confesses and you don’t, you’ll get the twenty, and he’ll walk. If neither of you confess, McCoy can’t make his case for the major crime, but he’ll make sure you both do two years for the minor one. What’s the right play?

Well, logically speaking, regardless of what your partner ends up doing, you’re better off confessing. But if you both confess, you both end up worse off than if you had both kept your mouths shut. If you had had the chance to communicate with each other, you might have chosen differently. The fact that you don’t know what your idiot partner is going to do while gazing into the eyes of the lovely ADA means that you can’t afford to take any chances, and neither can he. You both end up doing the nickel, even though neither of you had to.

In this example, you only get to play the game once. If you play some version of the Prisoner’s Dilemma with the same person repeatedly, your choices can affect future outcomes. In a sense, the choices you make are a form of communication. Only the very last time you play do you revert back to the original cutthroat scenario. (And since everybody knows this will be the case, the next-to-last iteration can also be cutthroat. How far back does this reasoning work?) There is actually a twenty-year-old Iterated Prisoner’s Dilemma competition for artificial intellegence programs and the winning strategy has long been the simple Tit-for-Tat. But it seems there’s now a new champion, though it seems to me to be a bit of a cheat. Read the article and let me know what you think.

The Prisoner’s Dilemma is an illustration of one of the central concepts of a branch of mathematics called “game theory.” Game theory allows us to make mathematical computations in decision making, even when all of the factors are not known. Think of two generals, one trying to choose a target to attack, the other deciding how to deploy defensive forces. Each knows the other is intelligent and out there making his decision. That’s game theory. If you were to meet someone anywhere in the world outside of the United States, but you couldn’t plan with that person ahead of time, where would you go? Would it surprise you to learn that almost everyone makes the same choice? (Post your answer in the comments section, if you like.) That’s game theory too.

With a branch of mathematics that can take unknown variables into account, a computer’s functionality can be increased significantly. Obviously computers that are powerful enough can play chess, but game theory allows them to play poker as well. There’s already a Texas Hold ‘Em Tournament for Artificial Intelligence programs. Imagine putting all of these programs into a giant simulated Texas Hold ‘Em Tournament where the losing programs died out and the winning programs created offspring with the possibility of mutation. We might evolve the ultimate strategy. And when we do, the first round of drinks are on me!

But as computers get more powerful, imagine other simulations we may be able to run, and what understandings we might be able to gain from these experiments. Evolution has proved itself to be a mighty force in the past. Once all of the data from Web 2.0 is compiled, maybe it will be allowed to evolve into Web 3.0. It’s not about computers becoming super-sentient and ruling over humans. It’s about humans developing and using new tools that can increase our capacity for growth. And if evolution has taught us nothing else, it has taught us that.

This week, 60 Minutes did a fascinating piece on a remarkable young man named Daniel Tammet:

Twenty-four years ago, 60 Minutes introduced viewers to George Finn, whose talent was immortalized in the movie “Rainman.” George has a condition known as savant syndrome, a mysterious disorder of the brain where someone has a spectacular skill, even genius, in a mind that is otherwise extremely limited.

Morley Safer met another savant, Daniel Tammet, who is called “Brain Man” in Britain. But unlike most savants, he has no obvious mental disability, and most important to scientists, he can describe his own thought process. He may very well be a scientific Rosetta stone, a key to understanding the brain.

Tammet has a condition known as synesthesia, which is when the brain gets its wires crossed, and two or more senses overlap. In some cases, days of the week might seem to the afflicted to have their own personalities (as they do here at Shakespeare Teacher). In other cases, particular years might, for an individual, occupy specific locations in space. In Tammet’s case, he can actually see numbers.

“I see numbers in my head as colors and shapes and textures. So when I see a long sequence, the sequence forms landscapes in my mind,” Tammet explains. “Every number up to 10,000, I can visualize in this way, has it’s own color, has it’s own shape, has it’s own texture.”

For Tammet, 289 is an ugly number. He describes 333 as very beautiful. Pi is “one of the most beautiful things in all the world.” In fact, Tammet holds the European record for reciting the digits of pi from memory, rattling off 22,514 digits without error in just over 5 hours. In my very best attempt, I have not been able to recite half that many.

Fans of the blog know me as an armchair brain science researcher, so I’m naturally fascinated by the idea of synesthesia. What other forms might it take? Could there be people who can smell the letters of the alphabet? Would a metaphor have a different taste than a hyperbole? Could you fall in love with a time of day? And would all people with the same kinds of synesthesia map their senses out the same way? We all know what a green square looks like, but would another person with Tammet’s brand of synesthesia agree with him about what 2,192 looks like? In other words, does 2,192 have an inherent visual representation and he’s the only one who can tell us what it looks like, or is his mind inventing its own unique schema to help it make sense of a neural configuration that was never supposed to happen? And if it’s the latter, what is the logic behind that system? Every question leads to more questions. But for scientists – um, real scientists – some of the answers may lie with Tammet himself.

There are maybe 50 savants alive today. These abilities generally go along with some kind of autism, making it difficult for researchers to interview the subjects and learn about the condition. But Tammet’s autism is very mild, and he’s able to articulate his experiences and provide researchers with a unique insight.

Tammet’s abilities, and disabilities, are described in much greater detail in this article in the Guardian from about two years ago, as well as some insight on what brain science researchers hope to gain from working with him:

Professor Simon Baron-Cohen, director of the Autism Research Centre (ARC) at Cambridge University, is interested in what Mänti might teach us about savant ability. “I know of other savants who also speak a lot of languages,” says Baron-Cohen. “But it’s rare for them to be able to reflect on how they do it – let alone create a language of their own.” The ARC team has started scanning Tammet’s brain to find out if there are modules (for number, for example, or for colour, or for texture) that are connected in a way that is different from most of us. “It’s too early to tell, but we hope it might throw some light on why we don’t all have savant abilities.”

The clip below is the second of two from a British documentary about Tammet. You can view the first one here if you’re interested. The clip below is just over eight minutes long. I’m including it here so you can see the first four minutes, where Tammet describes how he “sees” numbers. If you want to watch the last four minutes, though, you can see Tammet meet Kim Peek, the real-life person on whom “Rain Man” is based.